Summer 2023 Projects
The 2023 UC Davis Math REU will have several research projects (see below), representing various research areas of the UC Davis math department. Students will be directly mentored by UC Davis faculty and postdoctoral researchers, and will have the opportunity to interact with UC Davis. Students will be expected to give an oral presentation to their peers at the end of the program, and then write a final report.
Project 1: Matroid theory and optimization
Advisor: Luze Xu and Matthias Koeppe
Δ-modular matrices recently gain increasing interests in the analysis of optimization problems. They are integral matrices with pure combinatorial structure: the absolute value of the subdeterminants is bounded by a fixed constant Δ. In this project, we will start from the special case Δ=1, which is well-known as Totally-Unimodular (TU) matrices. We will learn Seymour’s decomposition theorem for TU matrices via matroid theory (which is an abstract theory of dependence capturing and generalizing properties from both linear algebra and graph theory), and learn how the TU property benefits integer optimization. Then we will learn recent results for bimodular (Δ=2) and beyond that. At the meantime, we will also research on the application of these structural properties, especially in the computational complexity of integer optimization with Δ-modular coefficient matrices. In this REU project, students will learn about the structure of Δ-modular matrices and explore the applications in combinatorics and optimization.
Project 2: Stability of quantum dynamics and circuits
Advisor: Bruno Nachtergaele
To describe and understand the behavior of quantum systems, one typically relies on mathematical models that incorporate the most important features while at the same time neglecting many others. Such an approach can only be successful if the resulting models have specific stability properties that guarantee that small modifications of its parameters will not qualitatively change its behavior. An important objective of the mathematical study of quantum systems is to establish sufficient conditions for the desired stability properties and to develop methods to verify that such conditions are satisfied.
The goal of the project is to become familiar with the mathematics of quantum systems and to investigate stability questions for specific models. REU participants in the project will learn and explore: linear algebra of complex vector spaces, tensor products, spectra of linear maps, perturbation theory for matrices, quantum dynamics, quantum circuits, quantum entanglement, and quantum spin chains and other basic quantum systems.

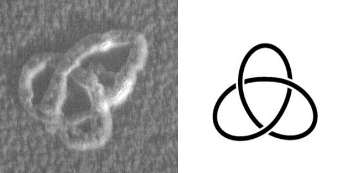
Project 3: Purifying and cataloguing DNA knots
Advisor: Javier Arsuaga
DNA knots are commonly observed as the product of enzymatic reactions or as a consequence of the spatial confinement of DNA. In some DNA viruses, called bacteriophages for their ability to propagate in bacteria, DNA knots with low crossing number have already been identified. This knot distribution is characterized by the absence of four crossing knots and a prevalence of torodidal knots over twist knots. Characterization of more complex knots however is still missing. In this project we will combine experimental molecular biology with computational/geometrical knot theory to purify DNA knots from bacteriophage P4 and study their mathematical properties. Our ultimate goal is to relate the properties of these knots to basic principles of DNA organization.
Project 4: Mysteries of algebraic numbers
Advisor: Motohico Mulase
We know integers and rational numbers quite well, or at least we feel so. The next stage of numbers is the field of algebraic numbers if we employ only algebraic methods to define them. It is defined as the set of all roots of polynomial equations with rational coefficients. In algebraic geometry, a family of deformations of algebraic varieties often produces linear differential equations whose coefficients are algebraic numbers, and at the same time, the behavior of their solutions are also controlled by algebraic numbers, the quantities known as monodromies, or periods.
How about its converse? If we have a system of linear differential equations defined over algebraic numbers, and their monodromies are also given by algebraic numbers, then can we find a geometry behind the scene? Can we say the differential equations come from a family of algebraic varieties? The idea here is a question, whether something is an algebraic number dictates the existence of geometry behind the scene.
Bonus: We will begin by discussing a proof of the transcendence of π and e. The idea comes from a simple linear differential equation with integer coefficients, and the period of the solution to this differential equation.